Теоретическое обоснование устойчивости метода

Настоящий раздел посвящён анализу устойчивости предложенного метода маскировки.

Предварительно дадим некоторые вспомогательные определения и теоремы. Пусть

. Пусть poly(n) - произвольный многочлен от переменной n.

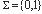
Определение 1. Пусть

, пусть m=poly(n). f называется односторонней функцией, если для любого полиномиального вероятностного алгоритма A и для любого

выполняется соотношение

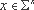
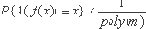
Определение 2. Взаимно-однозначная односторонняя функция

называется односторонней перестановкой.

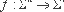
Определение 3. p-приближённым алгоритмом решения оптимизационной задачи называется алгоритм, находящий решение не более чем в p раз хуже оптимального решения.

Например рассмотрим задачу S минимизации некоторого функционала f. Пусть A - p -приближённый алгоритм нахождения решения задачи S. Пусть для некоторой реализации задачи оптимальное значение функционала равно X. Тогда алгоритм A найдёт решение задачи, при котором значение f равно Y, причём будет справедливо неравенство

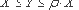
Определение 4. Пусть

. Пусть x=(x1....,xm), y=(y1....,yn), y=f(x). Переменная xk называется существенной, если существуют x1,...,kk-1,xk+1,...,xm

и j

{1,...,n} такие, что выполняется условие fj(x1,...,xk-1,0,xk+1,...,xm

fj(x1,...,xk-1,1,xk+1,...,xm ).

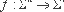
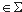
Теорема 1. Пусть

, f записана как система булевских формул в базисе

. Пусть

. Задача проверки существенности переменной xk (СУЩ) NP-полна.

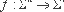
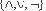
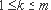
Доказательство. Введём обозначение

, где e1 e2 , - булевские формулы. Обозначим

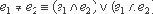
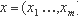
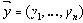
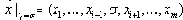
1. Покажем, что задача СУЩ находится в классе NP. Для этого построим булевскую формулу

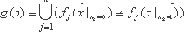
Если переменная существенна, то существует такой вектор

, для которого g(

)=1. Если переменная несущественна, то на всех наборах

выполняется g(

)=0. И наоборот, если g(

) принадлежит языку ВЫП, то переменная xk существенна, а если g(

) не принадлежит языку ВЫП, то xx - несущественна. Таким образом, задача проверки существенности сведена к задаче проверки выполнимости булевской формулы. Последняя находится в классе NP. Следовательно, и задача проверки существенности находится в классе NP.

2. Покажем, что к задаче СУЩ полиномиально сводится задача ВЫП, которая является NP-полной. Пусть

- некоторая формула в базисе

. Рассмотрим формулу, реализующую функцию f

1 . Она, очевидно, принадлежит языку ВЫП, но ни одна переменная в такой формуле не является существенной. В формуле, реализующей функцию f

0, которая не принадлежит языку ВЫП, также нет существенных переменных. Все прочие формулы, принадлежат языку ВЫП, и хотя бы одна переменная в них является существенной. Таким образом, формула не принадлежит ВЫП, если её значение на любом битовом наборе (например, на наборе

) равно 0, и в ней нет существенных переменных. Таким образом, для проверки выполнимости формулы нужно проверить её значение в одной точке и m раз проверить существенность переменных формулы. Таким образом задача ВЫП полиномиально по Тьюрингу сводится к задаче СУЩ, что доказывает NP-полноту последней.

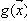
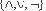
Определение 5. Пусть

, пусть ? - множество всех таких функций, и пусть

- оракульная функция

:? - > {0,1} такая, что для любой функции f

(f)=0, если f

(f)=1, в противном случае.

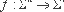
Обозначим через ?f формулу, реализующую функцию f. Пусть Ф - множество формул (потенциально бесконечное) такое, что если ?f - случайно и равновероятно выбранная формула из Ф, а f - функция, которую она реализует, то случайная величина

(f) принимает значение 1 с вероятностью p, а значение 0 с вероятностью q=1-p.

Множество формул Ф называется семейством непрозрачных предикатов, если для любого полиномиального вероятностного алгоритма A: Ф - > {0,1} выполняются условия

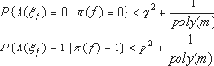
Теорема 2. Если непрозрачные предикаты существуют, то P

NP .

Доказательство. Пусть P = NP. Тогда существует полиномиальный алгоритм для решения задачи выполнимости, то есть существует алгоритм A, который для любой формулы ?f за полиномиальное проверит условие f

0 и выдаст ответ 0, если условие выполняется, и 1 в противном случае. Тогда P{A(?f)= 0|

(f)=0}=1, P{A(?f)= 0|

(f)}=1 , то есть непрозрачные предикаты не существуют. Полученное противоречие доказывает утверждение.

Мы можем расширить понятие непрозрачного предиката, предположив, что область его определения может быть произвольной (например, множество всех целых чисел, представимых определённым количеством битов). Покажем, что непрозрачные предикаты могут быть реализованы и с использованием указателей, и с использованием массивов.

Теорема 3. Если булевские непрозрачные предикаты существуют, то непрозрачные предикаты, построенные на указателях, существуют.

Доказательство. Пусть f - булевский непрозрачный предикат. Пусть f:

m - >

, f записана в базисе

. Построим следующее определение структурного типа на Си.

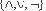
struct s { struct s *neg; struct s *min[2]; struct s *max[2]; };

Создадим в начале работы программы в динамической памяти ссылочную структуру, показанную на рис. 9.

Здесь элемент, на который указывает Pfalse, соответствует логическому значению "ложь", а элемент, на который указывает Ptrue, соответствует логическому значению "истина".

Рассмотрим каждую булевскую операцию и поставим ей в соответствие операцию над указателями в созданной структуре данных.

xi, где xi - булевская переменная. Ей соответствует переменная pi указательного типа struct s*, которая равна либо Ptrue, либо Pfalse.

u, где u - булевское выражение. Ему соответствует выражение указательного типа e->neg, где e - выражение, соответствующее u.

u v u, где u, v - булевские выражения. Такому выражению соответствует выражение указательного типа e->max[e == f], где e соответствует u, а f - v.

v, где u, v - булевские выражения. Такому выраженю соответствует выражение указательного типа e->min[e == f], где e соответствует u, а f - v.

Рис. 9: Схема построения непрозрачного предиката из указателей

Таким образом, каждому булевскому выражению u мы сопоставили выражение указательного типа e. Поскольку задача определения u

true NP-полна, то и задача определения e == Ptrue также NP-полна. Непрозрачному предикату f соответствует выражение указательного типа f, также являющееся непрозрачным предикатом.

Теорема 4.

Если булевские непрозрачные предикаты существуют, то и непрозрачные предикаты, построенные над массивами, существуют.

Доказательство. Пусть е - непрозрачный предикат над указателями, построенный, как показано в предыдущей теореме. Поставим ему в соответствие массив целого типа a из 10 элементов, заполненный следующим образом: int a[10] = { 5, 0, 0, 5, 0, 0, 0, 5, 5, 5 };

Указательному значению Pfalse соответствует целое значение 0, а указательному значению Ptrue - целое значение 5. Тогда выражения непрозрачного предиката, построенного на указателях, заменяются на индексные выражения по следующим правилам:

Переменная pi заменяется на переменную qi целого типа, которая может принимать значения из множества {0,5}.

Выражение e->neg заменяется на выражение a[b], где b - индексное выражение, соответствующее e.

Выражение e->min[f] заменяется на выражение a[b + 1 + c], где b - индексное выражение, соответствующее e, а c - индексное выражение, соответствующее f.

Выражение e->max[f] заменяется на выражение \V{a[b + 3 + c]}, где b - индексное выражение, соответствующее e, а c - индексное выражение, соответствующее f.

Определение 6. Пусть f:

m - >

n. Пусть

=(x1,...,xm),

=(y1,...,yn),

=f(

). Пусть . Множество I - это множество индексов интересующих нас компонент

. Переменная xk называется существенной относительно множества I, если существуют такие x1,...,xk-1,xk+1,...,xm

$ и такая j

I , что выполняется условие fj(x1,...,xk-1,0,xk+1,...,xm).

Теорема 5. Пусть даны m, n, f:

m - >

n, I

2(1,...,n), k. Задача проверки существенности переменной xk относительно множества I (СУЩМНОЖ) NP-полна.

Доказательство. Доказательство принадлежности задачи к классу NP аналогично доказательству теоремы 1. Для доказательства NP-полноты заметим, что задача СУЩ является частным случаем данной задачи, если мы выберем I={1,...,n).

Пусть V={v1,...,vk) - множество переменных замаскированной программы. Предположим, что базовый блок представляет собой вычисление булевской функции f:

m - >

n.

Пусть Vin

V,|Vin|=m - переменные, значения которых используются при вычислении f, а Vout

V, |Vout|=n - переменные, которые получают новые значения в результате вычисления. Если для некоторой переменной v

Vin и v

Vout, при вычислении используется старое значение переменной. Пусть Wout

Vout - множество "существенных" переменных на выходе из базового блока (например, это могут быть переменные, значения которых печатаются, или переменные, значения которых интересны нам по другой причине). Определим задачу анализа зависимостей по данным (ЗАВ) как задачу нахождения минимального множества переменных Win

Vin такого, что переменные из множества Vin - Win несущественны отностительно Wout.

Данной оптимизационной задаче соответствует задача проверки свойств ЗАВ: дано множество булевских переменных V={v1,...,vk}, булевская функция f:

m - >

n над переменными из Vin, подмножество Wout

Vout , число p (0

k). Существует ли множество Win

Vin , |Win|

p такое, что переменные Vin - Win несущественны отностительно Wout.

Теорема 6. Задача ЗАВ NP-полна.

Доказательство Принадлежность задачи классу NP следует из того, что для каждого i (1

k ) можем найти решение задачи СУЩМНОЖ, то есть определить принадлежит ли множеству Vin. Далее за полиномиальное время проверяется, что |Win|

p.

Для доказательства NP-полноты покажем, как задача СУЩМНОЖ сводится к данной задаче. Пусть f - булевская функция f:

m - >

n . Предположим для определённости, что f записана в виде КНФ. Для определённости будем считать, что x1=v1,...,xm = vm - переменные, используемые при вычислении функции, а y1 = vm+1,...,yn = vm+n - переменные, получающие своё значение. Пусть требуется проверить существенность переменной xk относительно множества I.

Введём m-1 новую переменную z1,...,zm-1 следующим образом: каждое вхождение xk в формулу для вычисления f заменим выражением xk v z1 v...v zm-1, а выражение - на выражение

. В результате получим функцию f1 :

2m-1 - >

n , которая также записана в КНФ.

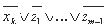
Если переменная xk существенна для f, то переменные xk,z1,...,zm-1 окажутся существенными для f1 .

Если переменная xk несущественная для f, то все переменные xk,z1,...,zm-1 несущественны для f1. С другой стороны, если хотя бы одна переменная из множества {xk,z1,...,zm-1} окажется несущественной в f1, то и все переменные этого множества будут несущественными.

В таком случае пусть p=m-1 . Тогда, если задача ЗАВ для функции f1 , множества переменных I и значения p даёт ответ "да", отсюда следует, что все переменные xk,z1,...,zm-1 несущественны, а если ответ "нет", то все эти переменные существенны.

Таким образом задача СУЩМНОЖ сводится к задаче ЗАВ, что показывает NP-полноту последней.

Рассмотрим оптимизационную задачу ЗАВ. Она состоит в нахождении такого Win

Vin , что p=|Win| минимально. Из NP-полноты задачи проверки свойств следует NP-трудность оптимизационной задачи.

Теорема 7. Если P

NP, то для любого p>1 не существует полиномиального p-приближённого алгоритма решения оптимизационной задачи ЗАВ

Доказательство. Пусть существует такое p>1 , что существует полиномиально-ограниченный алгоритм A, который находит множество существенных переменных WinA такое, что pA=|WinA|

P*p

n , где p - оптимальное решение. Очевидно, 0

P*p

n.

Рассмотрим следующую реализацию задачи СУЩ. Пусть f - булевская функция f:

m - >

n. Предположим для определённости, что f записана в виде КНФ. Для определённости будем считать, что x1=v1,...,xm=vm - переменные, используемые при вычислении функции, а y1=vm+1,...,yn=vm+n - переменные, получающие своё значение. Пусть требуется проверить существенность переменной xk относительно множества I.

Пусть [x] - минимальное целое число, не меньшее x. Введём l=m*[p] новую переменную z1,...,zl следующим образом: каждое вхождение xk в формулу для вычисления f заменим на выражение xk v z1 v ... v zl , а выражение

k - на выражение

. В результате получим функцию f1 :

m+1 - >

n , которая также записана в КНФ.

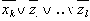
Обозначим через Win0 оптимальное решение оптимизационной задачи ЗАВ для формулы f, а через Win1 - оптимальное решение для формулы f1 .

Обозначим WinA решение, найденное алгоритмом A для f1.

Пусть xk - существенная переменная. Тогда Win0 таково, что 1+1

|Win0|

l*m , WinA таково, что , а удовлетворяет неравенству 1+1

|WinA|

l*m.

Пусть xk - несущественная переменная. Тогда Win0 таково, что 0

|Win0|

m-1, Win1 таково, что 0

|Win1|

m-1 , а WinA удовлетворяет неравенству 0

|WinA|

p*(m-1) .

Заметим, что p*(m-1)< l+1 =m*[p]+1 . В зависимости от WinA, полученного полиномиальным p-приближённым алгоритмом A мы можем определить, является ли xk существенной переменной или нет. Следовательно, P=NP.

Определение 7. Назовём "мёртвыми" все инструкции, которые относятся к вычислению несущественных переменных.

Из доказанного выше немедленно следует, что задача выявления мёртвого кода в программе, состоящей из одного базового блока, NP-полна, и, более того, для любого p>1 не существует p-приближённого полиномиального алгоритма выявления мёртвого кода.

Переменные произвольных целых типов могут рассматриваться как набор переменных булевского типа. Например, переменная типа int может рассматриваться как 32 булевские переменные, для доступа к которым используются битовые операции.

Содержание раздела